[컴퓨터 구조] Ch5. Digital Building Blocks (2) - Number System : Floating-point number 부동 소숫점 중심으로

Refrence : David Harris, Sarah Harris - Digital Design and Computer Architecture

목차

1. Arithmetic Circuits
2. Number Systems
3. Sequentail Building Blocks
4. Memory Arrays
5. Logic Arrays

Number Systems

여기서는 컴퓨터가 fraction을 어떻게 표현하는 지 배웁니다. 음수의 경우 2의 보수로 표현하면 되지만, 소수는 어떻게 표현해야 할까요? 소숫점이 고정이냐 유동적이냐에 따라 두 가지 방법으로 나뉩니다.

• Fixed-point
• Floating-point

(1) Fixed-point

6.75를 4 integer bits와 4 fraction bits로 표현하면, 0110.1100입니다.

이처럼 비트를 나눠서 소숫점을 고정하고 따로 표현하는 방법을 fixed-point라 합니다.

(2) Floating-point

273을 scientific notation으로 나타내면, 2.73 * 10^2 입니다. 이때, M= 2.73, B = 10, E = 2로 나타내면 다음 형식을 가집니다.

각각을 M : mantissa, B: base, E: exponent라고 합니다.

floating-point를 나타내는 국제 표준이 있습니다. 주의할 점은 Exponent에 bias를 더해주어야 하는 점입니다. 32bit 기준으로 bias는 127(01111111)입니다.

floating-point 변환 과정

1. 10진수를 2진수로 변환한다.
2. binary scientific notation으로 변환한다.
3. 32-bit floating point number의 필드에 각 비트를 채운다.

Example_1 : 228 변환

(1) 2진수 변환 : 228 = 11100100

(2) 11100100 = 1.11001 * 2^7

(3) 이때 E에 bias 127을 더해준다. 즉, 127 + 7 = 134 = 10000110 이다.

(4) 각 필드를 채워준다.

Example_2 : -58.25 변환

(1) -58.25 = 111010.01

(2) 111010.01 = 1.1101001 * 2^5

(3) 127 + 5 = 132 = 10000100

(4) 음수이므로 sign bit는 1이다.

Special Cases

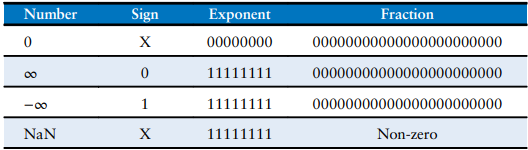
Single, Double precision

Additon

1. Extract exponent and fraction bits.
2. Prepend leading 1 to form the mantissa.
3. Compare exponents.
4. Shift smaller mantissa if necessary.
5. Add mantissas.
6. Normalize mantissa and adjust exponent if necessary.
7. Round result.
8. Assemble exponent and fraction back into floating-point number.

Example

0x3FC00000 + 0x40500000 = ??

우선, 완성된 floating point number를 다시 분해하는 과정을 거쳐야 합니다.

1. 16진수를 2진수로 변환
2. sign bit는 양수냐 음수냐에 따라 결정
3. 뒤에서부터 채운 후, 23bit는 Fraction, 나머지 8비트는 Exponent

위 과정을 통해 나타내면,

A = 0x3FC00000 = [0] [01111111] [100 0000 0000 0000 0000 0000]

B = 0x40500000 = [0] [10000000] [101 0000 0000 0000 0000 0000]

따라서,

A : S = 0, E = 127, F = .1

B : S = 0, E = 128, F = .101

1. F 앞에 1을 붙여서 Mantissa를 만든다.

1.1, 1.101

1. Exponent를 비교하여 자릿수를 맞춘다.

현재 각 E를 보면 127과 128이므로 A를 오른쪽으로 1bit만큼 shift합니다.

이때 bias인 127을 빼주고 각각을 나타내면,

0.11 * 2^1

1.101 * 2^1

이제 자릿수가 맞춰졌으니 둘을 더해줍니다.

⇒ 10.011 * 2^1

1. 정규화

10.011* 2^1 = 1.0011 * 2^2

1. Round

현재 F가 23비트 내로 들어오므로 round는 할 필요 없습니다.

1. floating-point format에 맞춘다.

1.0011 * 2^2을 기준으로 S, E, F를 구하면

S=0, E=2+127=129=10000001, F=0011………..(23bits)