Union-Find
Idea
유니온 파인드 알고리즘은 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘입니다.
노드를 합치는 Union 연산과 root 노드를 찾는 Find 연산으로 이루어집니다.
이러한 연산을 토대로 서로소 집합(공통 원소가 없는 두 집합) 자료 구조라 불리기도 합니다.

기차를 통해 출발지와 도착지를 정해서 이동이 가능한 지 판별하려고 합니다.
그래프를 통해 기차를 타고 서울에서 강릉으로 가는건 가능하지만 서울에서 부산으로 가는건 불가능하다는 것을 알 수 있습니다.
문제는 그래프가 복잡해지면 이러한 판단이 어려워 집니다. Union-Find 알고리즘을 이용하여 복잡한 그래프에서 두 노드가 연결되어 있는지 판별할 수 있습니다.
동작 과정

8개의 단절된 노드들이 있고, 이 노드들은 배열에 자기 자신의 값을 가지고 있다.

이 중에 1 2 노드를 연결하고 4 5 6 노드들을 연결하고 싶다.
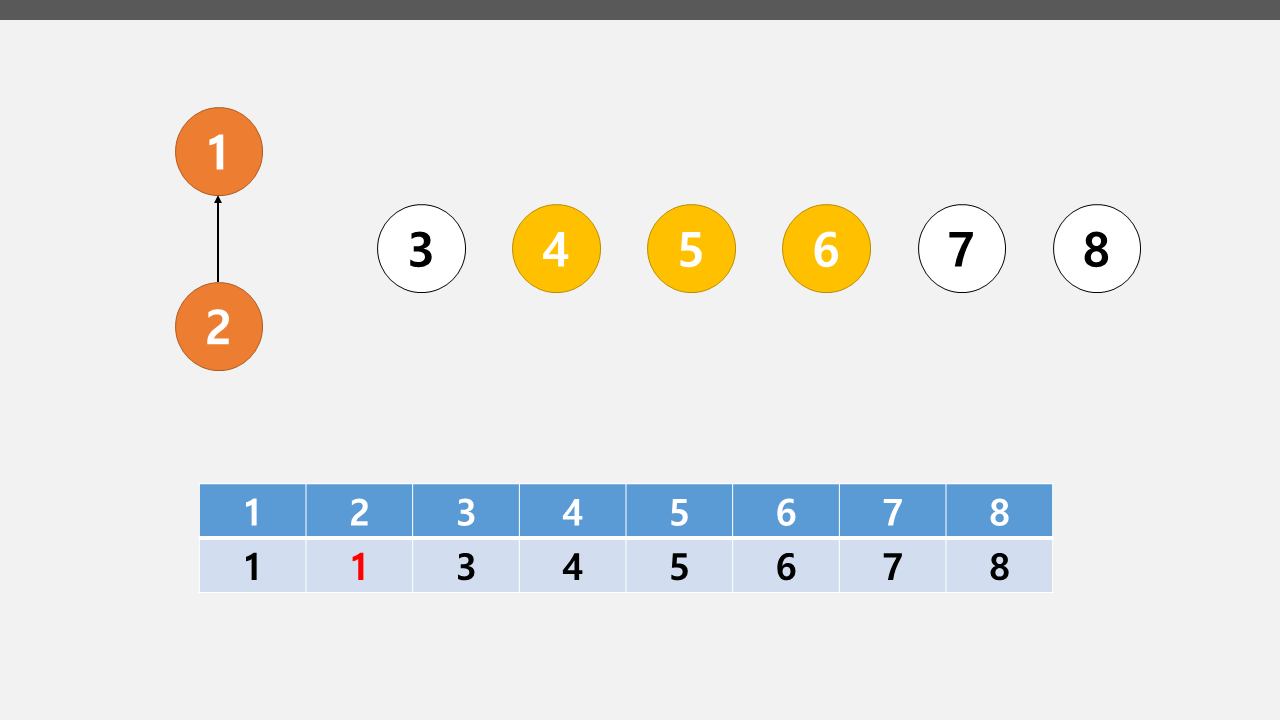
우선 1 2 노드를 합치기 위해 2번 노드의 배열 값을 1번 노드의 배열 값으로 바꾼다.
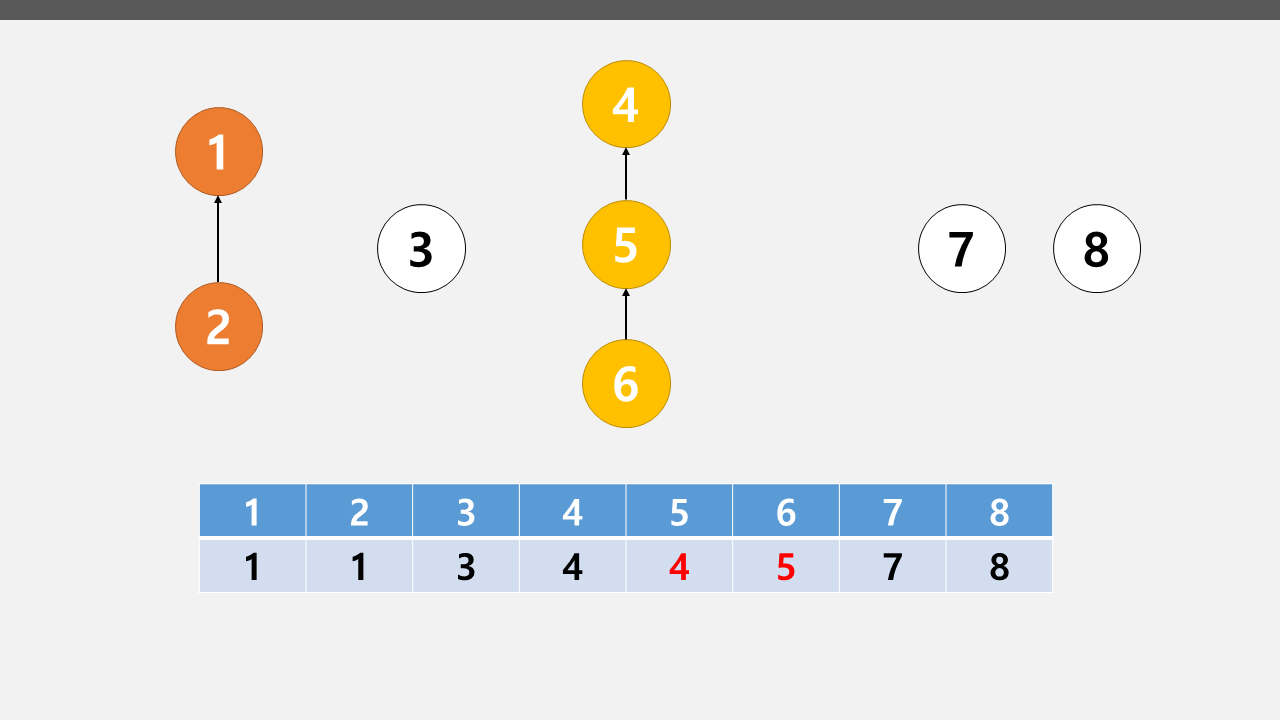
4 5 6도 마찬가지로 바꿔보자
4와 5를 연결하고 5와 6을 연결하면 그림처럼 배열이 바뀐다.
이때, 2번과 6번 노드가 연결되어 있는지 확인하고 싶다면
- 2번 노드의 부모를 찾는 과정
- 배열의 2번에 있는 값을 확인한다. 1번이다.
- 배열의 1번에 있는 값을 확인한다. 1번이다.
- 배열의 인덱스와 값이 일치한다.
- 그렇다면 1번 노드가 2번 노드가 속해있는 트리의 루트 노드이다.
- 6번 노드의 부모를 찾는 과정
- 배열의 6번에 있는 값을 확인한다. 5번이다.
- 배열의 5번에 있는 값을 확인한다. 4번이다.
- 배열의 4번에 있는 값을 확인한다. 4번이다.
- 배열의 인덱스와 값이 일치한다.
- 4번 노드가 6번 노드가 속해있는 트리의 루트 노드이다.
이제 각각 노드의 루트 노드를 비교해서 서로 다르다면 두 노드는 연결되어 있지 않은 것이다.
하지만 이렇게만 바꾸면 문제가 생긴다.
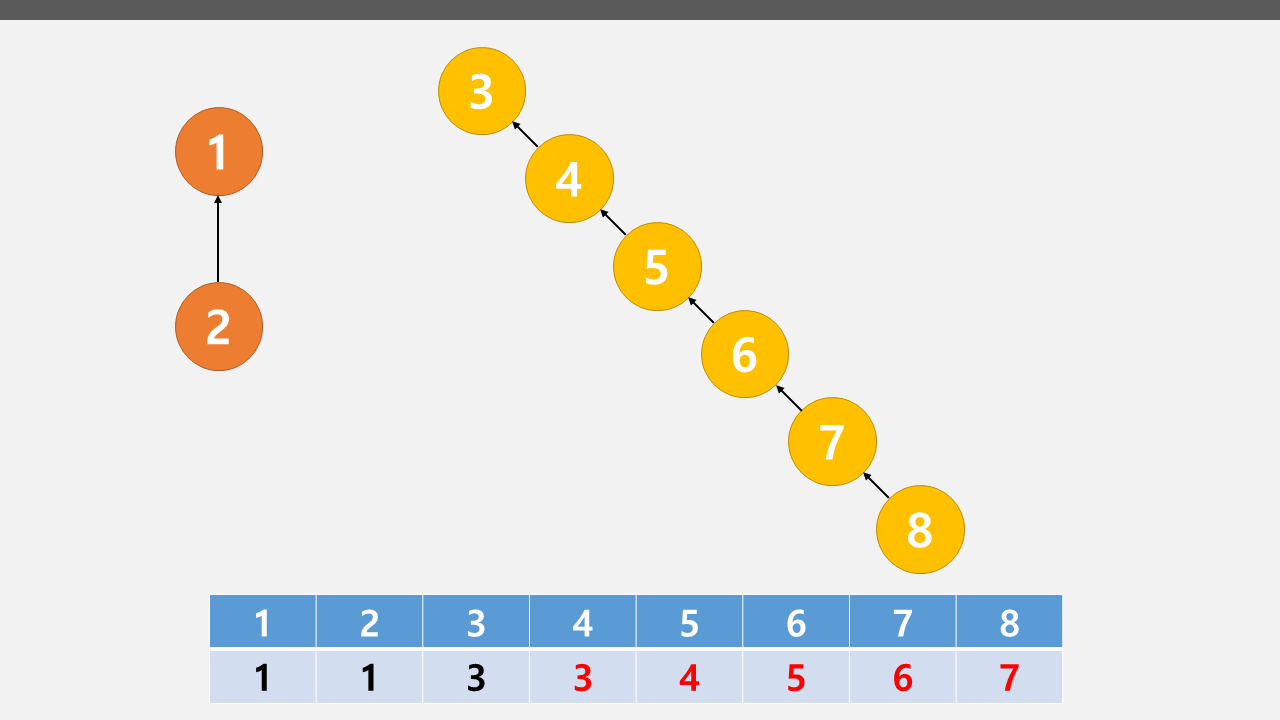
위의 예처럼 트리의 문제 중 하나인 한쪽으로만 자식이 몰려있는 편중현상이 생길 수 있는 것이다.
Find연산에서 재귀를 통해 루트 노드를 찾아야하는데 이렇게 편중되어 있으면 탐색하는데 시간이 많이 걸린다.
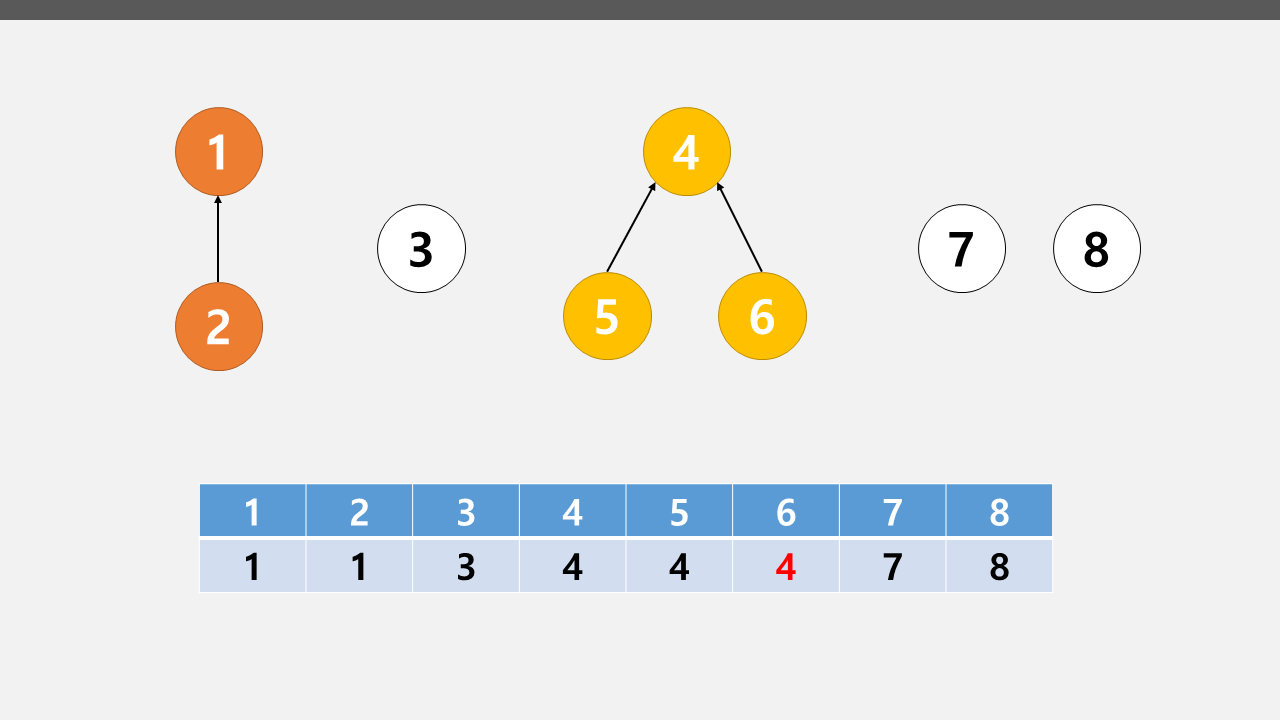
위의 편중 문제를 해결하기 위해 합치는 Union연산을 할 때
루트 노드를 찾는 탐색과정을 통해 루트노드에 연결하는 과정을 거쳐
결과적으로 위의 그림처럼 트리가 형성된다.
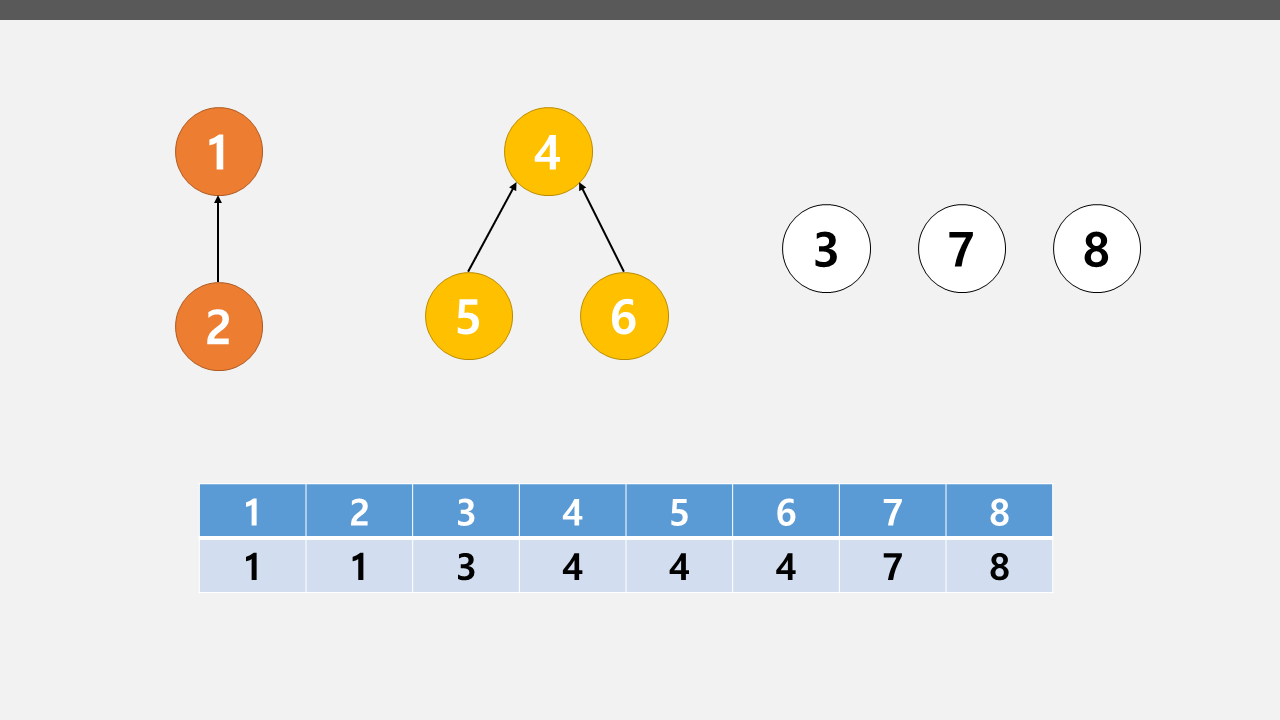
1 2 를 연결하고 4 5 6을 연결한 유니온 파인드의 트리구조이다.
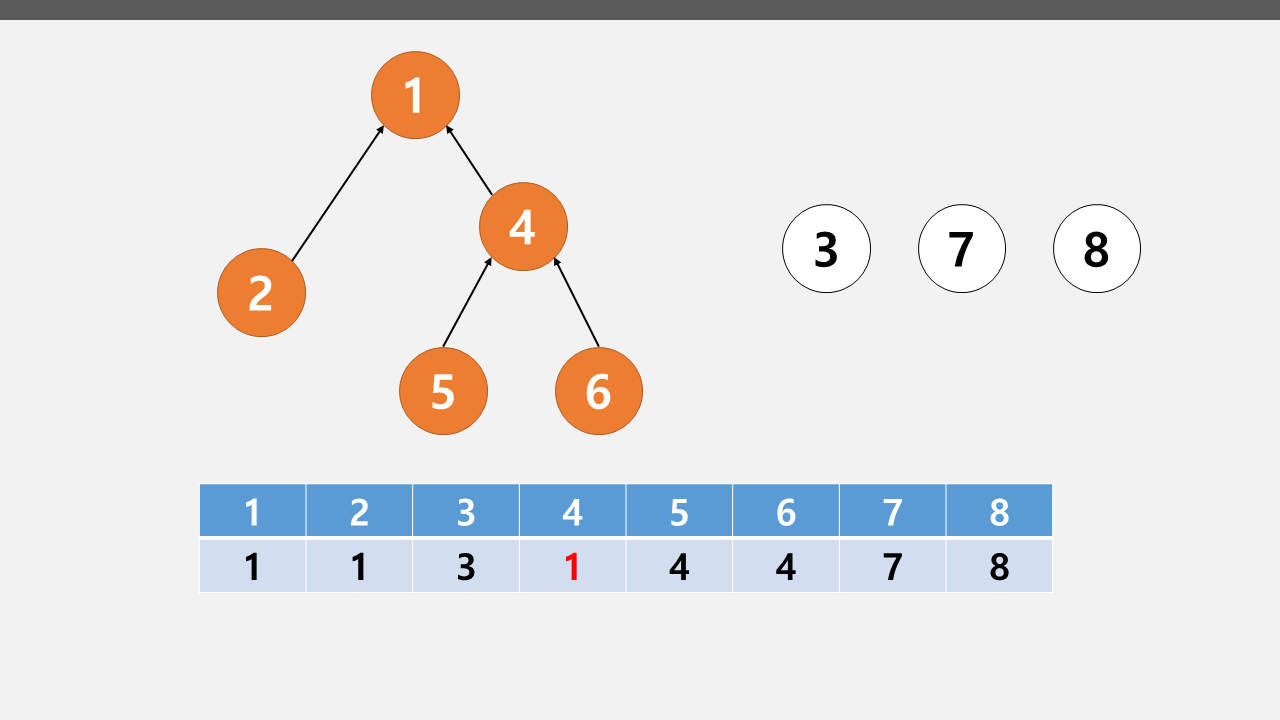
이제 1과 4번 노드를 연결하고 싶다면 위의 그림처럼 바뀔 것이다.
Code
# 특정 원소가 속한 집합을 찾기
def find(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
return find(parent, parent[x])
return parent[x] // 경로 압축을 이용한 최적화
# 두 원소가 속한 집합을 합치기
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
Time Complexity
유니온 파인드의 시간 복잡도는 최적화 여부, 순서 등에 따라 매번 달라집니다.
코드를 살펴보면 전체 시간 복잡도와 Union 함수의 시간 복잡도는 Find 함수의 시간 복잡도에 따라 결정됩니다.
경로 압축 최적화를 하지 않은 경우, 트리가 한 쪽으로 치우칠 수 있기 때문에 Find 함수의 시간 복잡도는 최악의 경우 O(N)이고, 경로 압축 최적화를 한 경우, 트리가 짧고 넓은 형태가 될 가능성이 높아지므로 O(logN) 입니다.
실제 시간 복잡도는 O(α(N))라고 한다. α(x)는 애커만 함수라고 하는데, x가 2의 65536제곱일 때 함수 값이 5가 된다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 크루스칼 (Kruskal) 알고리즘 (0) | 2023.05.22 |
|---|---|
| [Algorithm] Spanning Tree와 MST (Minimum Spanning Tree) (0) | 2023.05.22 |
| [Algorithm] 플로이드 워셜 (Floyd-Warshall) 알고리즘 (0) | 2023.05.15 |
| [Algorithm] 벨만-포드 (Bellman-Ford) 알고리즘 (2) | 2023.05.08 |
| [Algorithm] 다익스트라(Dijkstra) 알고리즘 (2) | 2023.05.08 |
![[Algorithm] 유니온 파인드 (Union-Find) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbeNh1g%2Fbtsf3qoDjzY%2FAAAAAAAAAAAAAAAAAAAAACgL4Em2_rNV682fVTVofCywWtQasZbIbuhlEpPj0Mbs%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D%252BoQg403CUkTi1tbiKCoiUSdW9ps%253D)