Dijkstra Algorithm
Idea
다익스트라 알고리즘은 그래프에서 한 정점에서 모든 다른 정점까지의 최단 경로를 구하는 알고리즘입니다.
매번 최단 경로의 정점을 선택하며 탐색을 반복함으로써 출발 정점에서 나머지 각 정점까지의 최단 경로를 모두 찾게 됩니다. 단, 모든 링크의 가중치(길이)는 양의 정수 값이어야 합니다!
이러한 최단 경로(최소 비용)을 구하는 알고리즘은 다익스트라 알고리즘 외에도 벨만-포드, 플로이드-워샬 알고리즘 등이 있습니다.
경로 계산 방식에는 아래와 같은 종류가 있습니다.
1. (One-To-One) 한 지점에서 다른 특정 지점까지의 최단경로 구하기
2. (One-To-All) 한 지점에서 다른 모든 지점까지의 최단경로 구하기
3. (All-To-All) 모든 지점에서 모든 지점까지의 최단경로 구하기
다익스트라 알고리즘은 이 중 2번째 유형(One-To-All) 입니다.
만약 음의 가중치가 있다면 벨만 포드를 사용해야 합니다.
음의 가중치가 있으면 안되는 이유

다음과 같은 경우에 다익스트라 알고리즘은 A->B->D 총 비용 22가 가장 최소 경로라고 생각 할 것입니다.
하지만 A->B->C->D가 총-90 으로 값이 더 작습니다.
즉, 위와 같이 음의 가중치가 포함된 그래프의 최단 경로는 다익스트라 알고리즘으로 구할 수 없는 경우가 있습니다.
다익스트라 알고리즘의 구현 방식에 따라 구할 수도 있고 못 구할 수도 있습니다. 자세한 내용은 아래 블로그를 참고해 주세요!
https://kangworld.tistory.com/76
동작 과정
- 출발 노드와 도착 노드를 설정하여 "최단 거리 테이블"을 초기화한다.
- 현재 위치한 노드의 인접 노드 중에서 방문하지 않은 노드들 중 거리가 가장 짧은 노드를 선택한다. (방문 처리)
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 갱신 : 현재 테이블의 최단거리보다, 해당 노드를 거쳐가는 비용이 작으면 작은 경로로 교체
- 2번과 3번 과정을 반복한다.
최단거리 테이블은 각 노드에 대해 주어지며, 각 값들은 1번 노드에서 x번 노드로 가는 최단 경로를 의미합니다.
처음에는 1번노드에서 자기 자신의 거리는 0이고, 나머지는 무한(INF)값으로 초기화합니다.

Step1

출발 노드인 1번 노드를 선택하고, 인접 노드인 2번과 3번의 거리를 계산하여 갱신합니다. 아직까지는 무한값이 들어있으니 각각 3과 4로 테이블 값이 업데이트 됩니다.
Step2
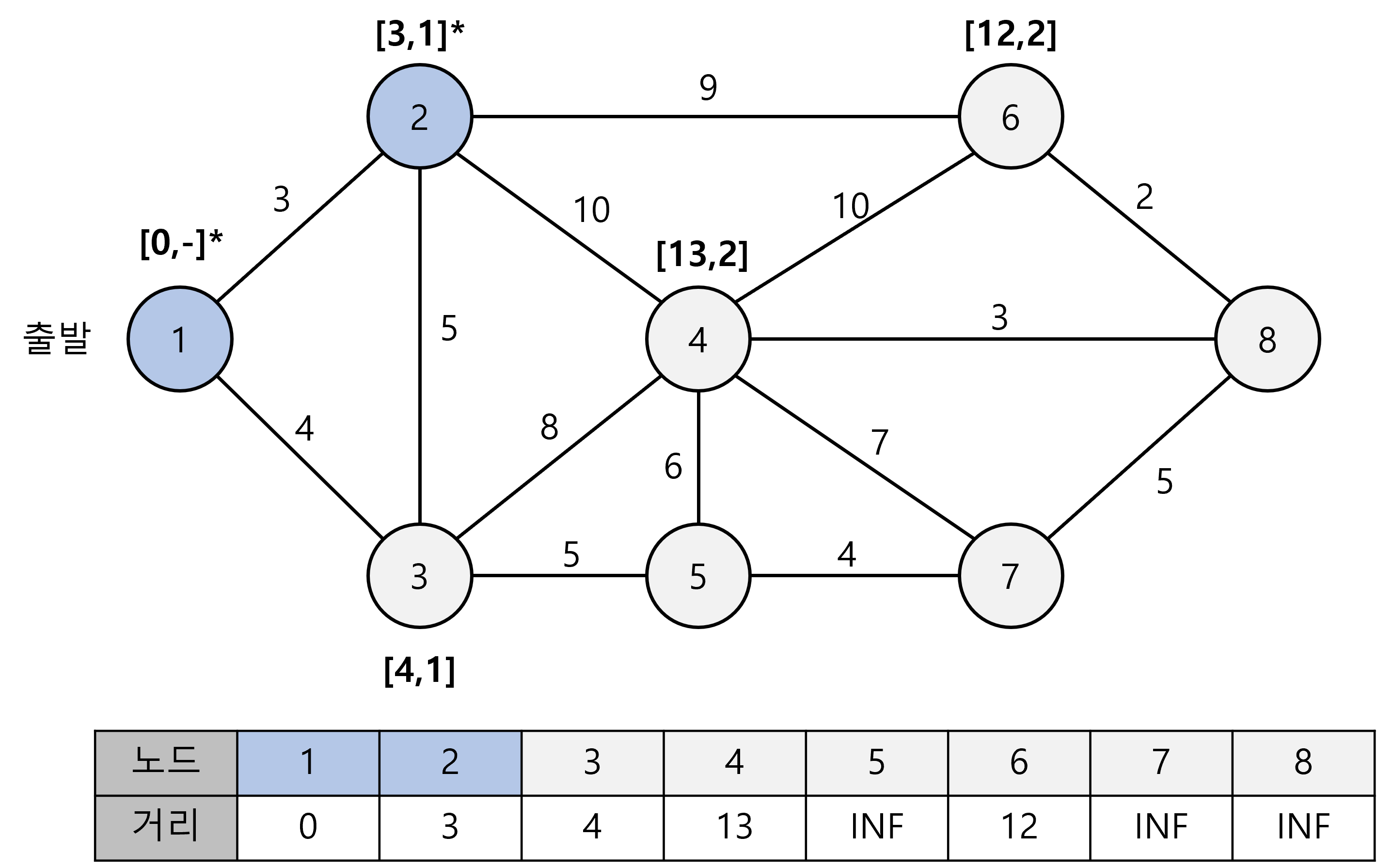
방문하지 않은 노드 중 가장 짧은 최단거리 노드인 2번을 선택하고, 2번 노드를 거쳐갈 수 있는 다른 노드들의 테이블 값을 갱신합니다. 3,4,6번 노드가 이에 해당합니다.
이때, 3번 노드는 1번 노드를 거치는 것은 더 비용이 싸므로 업데이트를 하지 않습니다. 하지만, 4번과 6번은 기존에 무한값이 들어있었기때문에 2번 노드를 거치는 경로의 비용으로 테이블 값을 업데이트합니다.
이제 3,4,6 번 노드 중에서 가장 짧은 최단거리 노드인 3번을 선택하고 2번 과정을 반복합니다.
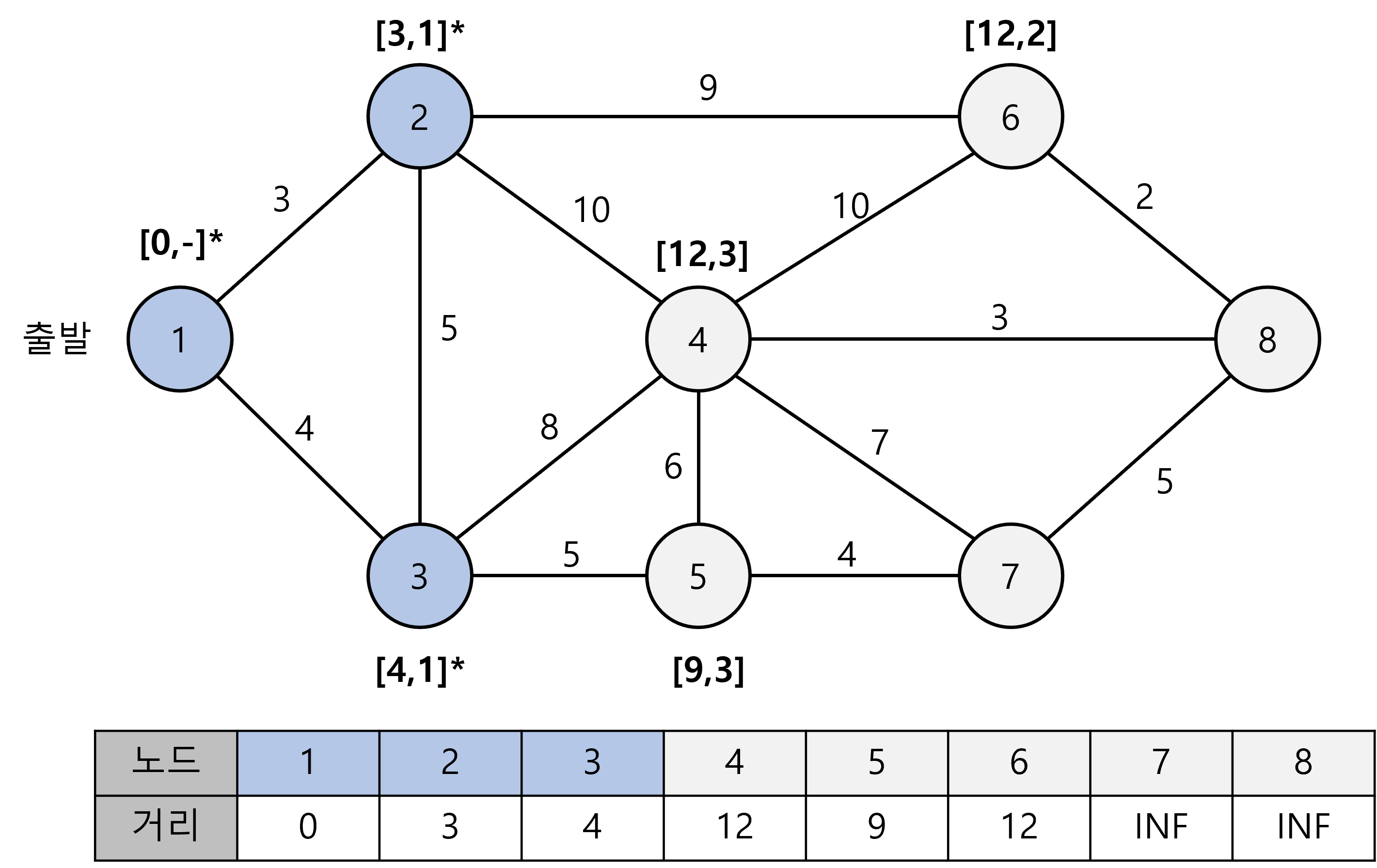
3번 노드에 대해서도 아직 방문하지 않은 4번과 5번의 최단 거리를 갱신해줍니다.
따라서 4번 노드의 테이블 값은 13 -> 12로 갱신됩니다.
Step3
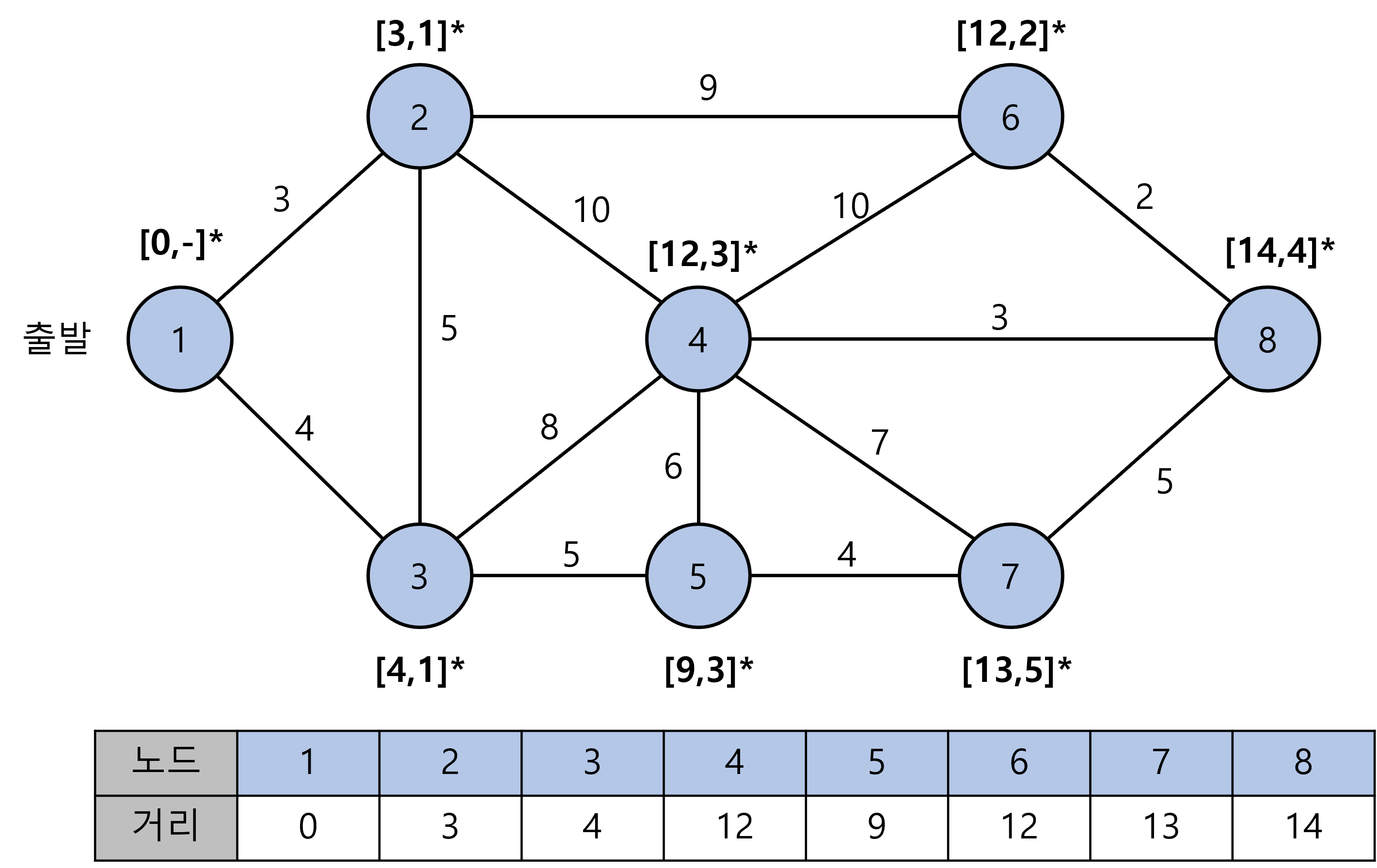
위 과정을 반복하면 최종 테이블은 위와 같습니다.
이로써 1번 노드에서 2~8번 노드까지의 최단 거리를 모두 구했습니다!
Code
import heapq
INF = int(1e9)
n,m = 8,14 # 노드 수
start = 1 # 출발 노드
graph=[[] for i in range(n+1)]
# 최단거리 + 부모노드 저장 테이블 생성
distance=[[INF,i] for i in range(n+1)]
# 양방향 입력
# 노드 a와 노드 b의 비용 c
for _ in range(m):
a,b,c = map(int, input().split())
graph[a].append((b,c))
graph[b].append((a,c))
def dijkstra(start):
q=[]
heapq.heappush(q,(0,start))
distance[start][0]=0
while q:
# 가장 최단거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 처리된적이 있는 노드라면 pass
if distance[now][0]<dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
# 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]][0]:
distance[i[0]][0]=cost # 최단거리 갱신
distance[i[0]][1]=now # 부모노드 저장
heapq.heappush(q,(cost,i[0]))
파이썬의 heapq를 통해 최소 힙 구조를 이용하여 다익스트라 알고리즘을 구현할 수 있습니다.
최소 힙을 통해서 거리가 가장 작은 튜플이 우선 추출되는 우선순위 큐를 구현함으로써 다익스트라 알고리즘을 작동시킵니다. 즉, 매번 모든 노드를 확인하여 최단거리 노드를 선택할 필요 없이, 우선순위 큐에 노드를 넣음으로써 항상 거리가 가장 작은 튜플이 추출되도록 합니다.
최소 힙으로 구현한다면 매번 루트 노드가 최소 거리를 가지는 노드가 되기 때문이다!
- 출발노드를 우선순위 큐에 넣는다.
- 우선순위 큐에서 데이터를 추출한다.
- 이미 갱신된 노드라면 Pass한다.
- 우선순위 큐에서 꺼낸 노드를 기준으로 방문할 수 있는 다른 노드들의 최단 거리 테이블을 갱신하고 큐에 담는다.
- 1~4를 반복한다.
Time Complexity
1. 우선순위 큐 사용
간선의 수를 E(Edge), 노드의 수를 V(Vertex)라고 했을 때, 다익스트라 알고리즘의 시간 복잡도는 가 됩니다.
우선 (1) 각 정점마다 인접한 간선들을 모두 검사하는 작업과 (2) 우선 순위 큐에 간선을 넣고 빼는 작업이 있습니다.
각 정점은 1번씩만 방문되므로, 모든 간선을 검사하면 O(E)의 시간이 걸립니다.
또한, 우선순위 큐에 간선들을 넣고 빼는 과정은 총 logE가 걸리므로(Heap 사용) 모든 간선을 우선순위 큐에 넣고 뺸다고 했을 때 총 O(ElogE)의 시간이 걸립니다.
이때, 그래프에서 중복 간선을 포함하지 않는다면 E는 항상 V^2 이하입니다. (모든 노드가 연결되어있는 경우 V(V-1))
따라서, logE < log(V^2) = 2logV 이므로, O(logV)로 표현할 수 있습니다.
최종적인 다익스트라 알고리즘의 전체 시간 복잡도는 O(ElogV)로 나타낼 수 있습니다.
2. 선형 탐색을 통한 구현
우선순위 큐를 사용하지 않고, 매번 반복문을 이용하여 방문하지 않은 노드 중 최단 거리 노드를 고르는 방식으로 구현할 수 있습니다. 이때는 총 O(V)번에 걸쳐서 모든 인접 노드를 살펴보기 때문에 시간 복잡도는 O(V^2) 가 됩니다.
Reference
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 플로이드 워셜 (Floyd-Warshall) 알고리즘 (0) | 2023.05.15 |
|---|---|
| [Algorithm] 벨만-포드 (Bellman-Ford) 알고리즘 (2) | 2023.05.08 |
| [Algorithm] 이진 탐색(Binary Search) 알고리즘 (0) | 2023.01.28 |
| [Algorithm] 위상 정렬(Topological sort) 알고리즘 (0) | 2023.01.28 |
| [Algorithm] 힙 정렬(Heap sort) 알고리즘 (0) | 2023.01.28 |
![[Algorithm] 다익스트라(Dijkstra) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fw3YOl%2FbtseqYtnVTb%2FeXiKh88Gs0zNV1JLHm4PYk%2Fimg.png)