반응형
Counting sort
Idea
- 가장 작은 데이터부터 가장 큰 데이터까지의 범위가 모두 담길 수 있는 리스트를 생성
- 데이터를 하나씩 확인하며 데이터의 값과 동일한 인덱스의 데이터를 1씩 증가
- 증가된 리스트에서 0인 값을 제외하고, 인덱스를 인덱스 값만큼 출력
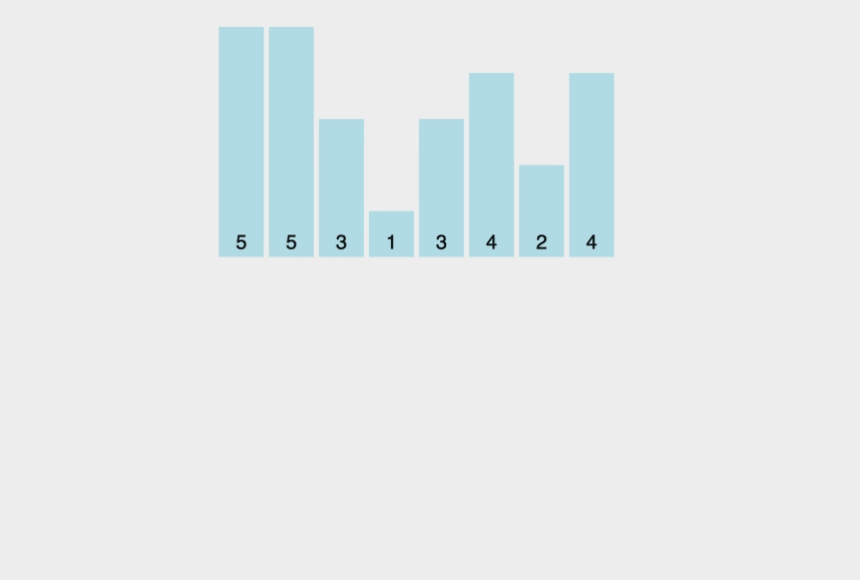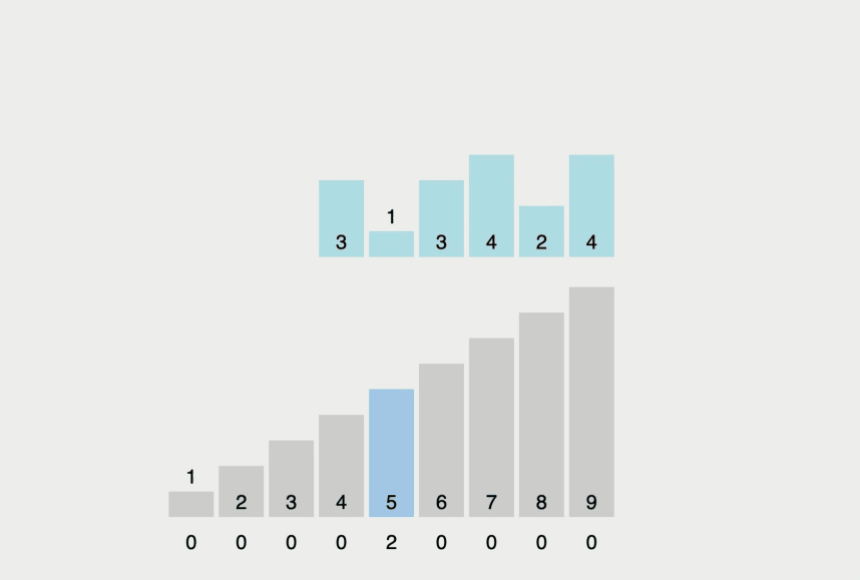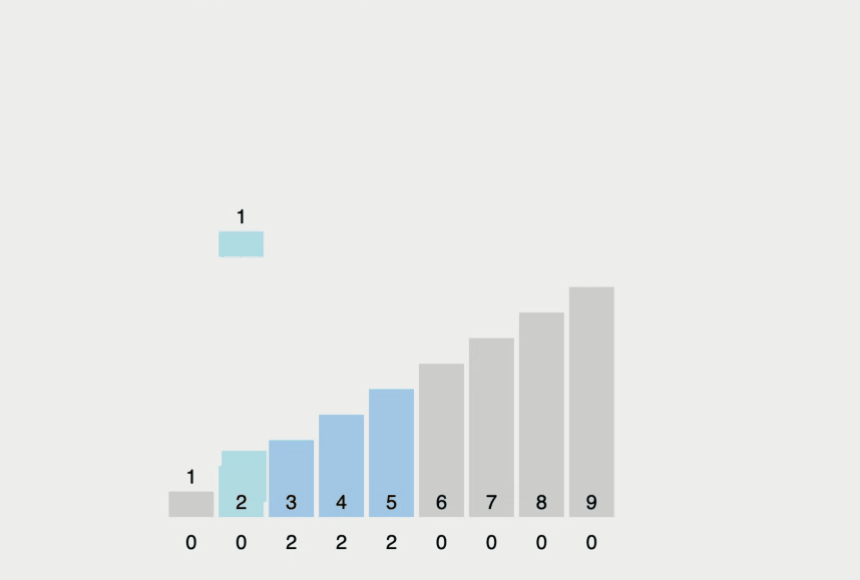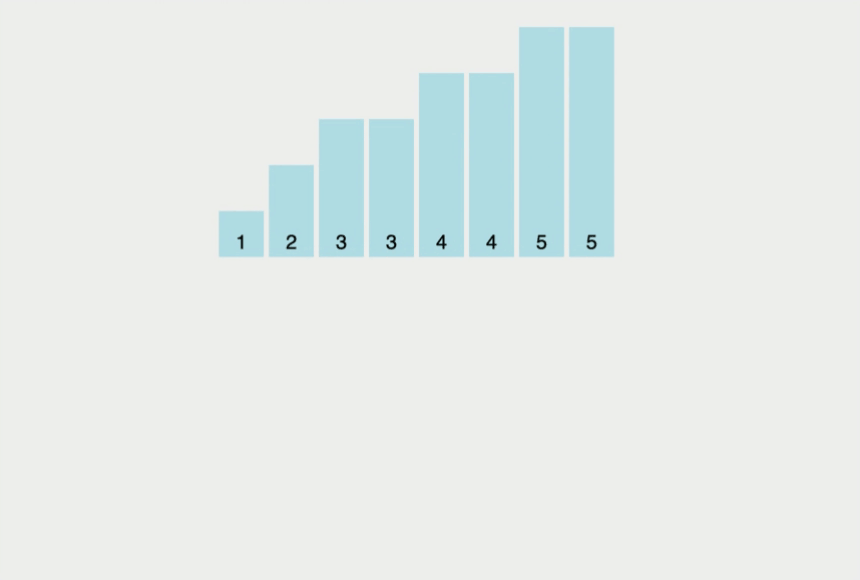
간단히 정리하면, 주어진 리스트들의 수들이 몇 번 나왔는지 기록한 후, 앞에서부터 차례대로 나온 횟수만큼 출력하는 것입니다.
When we use
계수 정렬은 다음의 제약 사항을 갖습니다.
- 데이터가 양수여야 한다.
- 값의 범위가 적당해야 한다. (메모리 issue)
이러한 제약 사항을 위반하지 않을 때, 값의 범위가 작은 경우 계수 정렬은 뛰어난 성능을 보입니다.
여타 다른 정렬 알고리즘을 살펴보면, 항상 비교 연산이 포함됩니다. 이러한 비교 연산은 시간 복잡도가 O(n)이므로 비교 연산을 사용하는 정렬 알고리즘은 아무리 빨라도 O(nlogn)의 시간 복잡도를 가지게 됩니다.
하지만, 계수 정렬의 경우 앞에서 살펴 보셨듯이 비교 연산을 사용하지 않습니다. 하지만 항상 trade off가 존재하듯이, 계수 정렬의 경우 속도가 빠른 대신 메모리를 많이 사용하게 되므로 범위가 넒은 input에 대해서는 사용할 수 없습니다.
따라서, 계수 정렬은 "값의 범위가 적당히 작을 때" 사용한다면 좋은 성능을 보일 것입니다.
Code
def counting_sort(arr):
max_arr = max(arr)
count = [0] * (max_arr + 1)
sorted_arr = list()
for i in arr: # 카운팅
count[i] += 1
for i in range(max_arr + 1):
for _ in range(count[i]):
sorted_arr.append(i)
return sorted_arr
Time complexity
우선, 전체 리스트를 탐색하고 정렬된 리스트를 얻는 연산들은 각각 O(n)이 소요됩니다.
하지만 이때, 계수 정렬의 특성 상 입력이 어떻게 주어지던지 항상 최대값만큼의 리스트를 생성해야 합니다.
최대값을 K라고 하면 길이가 K인 리스트를 무조건 생성해야 하기 때문에 K가 굉장히 클 경우 정렬 시간은 K에 의존하게 됩니다.
따라서 계수 정렬의 시간복잡도는
반응형
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 위상 정렬(Topological sort) 알고리즘 (0) | 2023.01.28 |
|---|---|
| [Algorithm] 힙 정렬(Heap sort) 알고리즘 (0) | 2023.01.28 |
| [Algorithm] 합병 정렬(merge sort) 알고리즘 (0) | 2023.01.23 |
| [Algorithm] 퀵 정렬(Quick sort) 알고리즘 (0) | 2023.01.19 |
| [Algorithm] 선택 정렬, 버블 정렬, 삽입 정렬 알고리즘 (0) | 2023.01.19 |
![[Algorithm] 계수 정렬(Counting sort) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcQkEbc%2FbtrWYMKE9lq%2FH8xsnvtMF2FCTZirf4HVhk%2Fimg.gif)