반응형
Merge sort
Idea
합병 정렬은 하나의 리스트를 크기가 균등한 리스트 두 개로 분할하고, 각 부분 리스트를 정렬(정복)한 후 다시 합병하는 방식입니다. 구체적으로 단계를 나누면 다음과 같습니다.
- 분할(Divide): 주어진 리스트를 같은 크기의 부분 리스트 2개로 분할한다.
- 정복(Conquer): 더 이상 분할이 불가능할 경우, 주어진 부분 리스트를 정렬한다.
- 결합(Combine): 정렬이 완료된 부분 리스트들을 다시 하나의 완전한 리스트로 합친다.
Example

위에서 살펴본 3단계 중, 1단계인 분할의 경우 주어진 리스트를 같은 크기로 2개 나누는 일이므로 특별한 연산이 필요하지 않습니다. 하지만, 2,3 단계의 경우 특별한 연산이 들어가고 사실상 하나의 단계로써 구현됩니다. 즉, 합병 정렬을 구현하기 위해서는 "합병" 과정에 집중해야 합니다.
합병 과정은 아래와 같이 진행됩니다.

- 부분 리스트들을 합병하는 과정에서 합병의 결과물을 담아둘 리스트(sorted)을 생성한다.
- 2개의 부분 리스트에 속한 원소들을 아래의 과정을 거쳐서 하나씩 비교한다.
- 각 부분 리스트의 최상단 원소끼리 비교한다.
- 둘 중 작은 값을 sorted로 이동시키고, 해당 인덱스를 1 증가시킨다.
- 1번과 2번 과정을 두 부분 리스트 중 하나가 빌 때까지 반복한다.
- 만약 3번 과정이 끝난 후에 어느 부분 리스트가 남아 있다면, 해당 부분 리스트의 원소들을 모두 sorted로 옮긴다.
여기서 중요한 점은, "부분 리스트는 이미 정렬이 완료된 상태이다."라는 것을 이용한다는 점입니다. 이러한 사실이 있기에 부분 리스트의 왼쪽에서 부터 하나씩 비교하는 것이 가능했던 것입니다.
그림에서는 표현이 안 됐지만, 가장 먼저 합병 과정이 일어나는 부분은, "부분 리스트의 길이가 1인 경우"에서 부터 시작할 것입니다. 그럼 길이가 2인 부분 리스트가 생성이되고, 이러한 길이 2짜리 부분 리스트들이 모이면 다시 합병 과정을 거쳐 길이가 4인 부분 리스트들이 생성됩니다. 이 과정을 쭉 거치면 언젠가는 최종적으로 완전히 정렬된 리스트를 얻을 수 있습니다. (길이는 2-4과정에 의해서 주어진 리스트에 따라 본 예시와 달라질 수 있습니다.)
Code
def merge_sort(arr, first, last):
if first >= last:
return
merge_sort(arr, first, (first+last)//2)
merge_sort(arr, (first+last)//2+1, last)
return merge(arr, first, last)
def merge(arr, first, last):
mid = (first + last) // 2
i, j = first, mid+1
temp = []
while i <= mid and j <= last:
if arr[i] <= arr[j]:
temp.append(arr[i])
i += 1
else:
temp.append(arr[j])
j += 1
while i <= mid:
temp.append(arr[i])
i += 1
while j <= last:
temp.append(arr[j])
j += 1
for k in range(first, last+1):
arr[k] = temp[k-first]
return arr
Time complexity
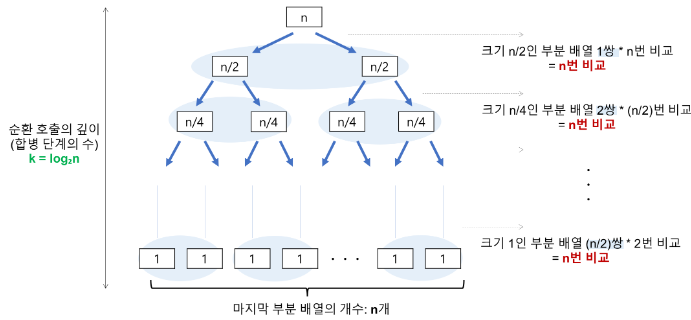
- 주어진 리스트의 size가 n일 때, 첫 부분 리스트들의 size는 n/2이 됩니다. 따라서 이들의 비교를 위해서는 n번의 비교 연산이 필요합니다. 다시 이를 분할하면 부분 리스트의 size는 n/4가 되고 비교 연산은 n/2이 필요합니다.
이를 일반화 시키면, 각 합병 단계에서는 최대 n번의 비교 연산을 수행한다고 정리할 수 있습니다. - n에 가까운 2의 거듭제곱 수를 M = 2^k 라고 하면, M의 총 병합 단계 횟수는 k번입니다.
이때 정의에 따라 k = log2M 이고, log2M ~= log2n 로 근사할 수 있으므로 총 비교 연산의 횟수는 nlog2n 입니다. - 추가로, 각 합병 단계에서 임시 배열을 거치기 때문에 size n에 대해서 총 2n의 이동 연산이 필요합니다.
즉, 총 이동 연산 횟수는 2nlog2n 입니다. - 따라서 최종 시간 복잡도는 3nlog2n -> O(nlog2n) 입니다.
반응형
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 위상 정렬(Topological sort) 알고리즘 (0) | 2023.01.28 |
|---|---|
| [Algorithm] 힙 정렬(Heap sort) 알고리즘 (0) | 2023.01.28 |
| [Algorithm] 계수 정렬(Counting sort) 알고리즘 (0) | 2023.01.27 |
| [Algorithm] 퀵 정렬(Quick sort) 알고리즘 (0) | 2023.01.19 |
| [Algorithm] 선택 정렬, 버블 정렬, 삽입 정렬 알고리즘 (0) | 2023.01.19 |
![[Algorithm] 합병 정렬(merge sort) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FWf9cV%2FbtrWXjWerhX%2FkKvnkMzaVjM4HRj0ZArerK%2Fimg.png)