[컴퓨터 구조] Ch5. Digital Building Blocks (1)- Arithmetic Circuits
Refrence : David Harris, Sarah Harris - Digital Design and Computer Architecture
목차
- Arithmetic Circuits
- Number Systems
- Sequentail Building Blocks
- Memory Arrays
- Logic Arrays
Arithmetic Circuits
(1) Adders
Carry Propagate Adder, CPAs 종류 : Ripple-carry, Carry-lookahead, Prefix
Carry-lookhead와 Prefix는 더 빠르지만 하드웨어 resource를 더 많이 사용합니다.
Ripple-carry adder (RCA)
1-bit adder를 연속적으로 이어 붙여서 만든 adder입니다. carry를 각각 이어서 받기 때문에 느립니다.
n-bits RCA는 full adder를 n개 연결시켜 만드는 가산기인데 여기서 n이 커질수록 full adder 연결사이에서 delay가 발생하게 되어 연산속도가 더 느려집니다.
Ripple-carry adder Delay

Carry-Lookahead Adder (CLA)
CLA는 generate와 propagate 두 가지의 신호로 이루어져 있고 이 둘을 통해 carry를 앞서 보고 계산할 수 있습니다.
즉, 각 자리에서 Carry 연산을 수행하는 방법입니다.
- Carry generationA 와 B 가 1이면 다른 stage와 무관하게 항상 carry 발생한다.
- G = A • B
- Carry Propagation P = A + B
- A 와 B 중 하나만 1이면 아래 stage로 부터의 carry 입력이 carry 출력으로 전파된다.
- Carry 계산
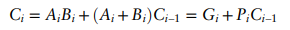
식을 살펴보면 다음 Carry는 G가 1이면 무조건 1이고, 이전 Carry가 1이더라도 P가 1이어야 현재 Carry로 전파됩니다. 이 둘을 or 조건으로 연결한 것입니다.
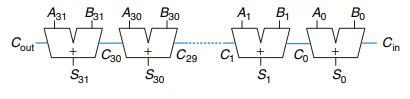
C_i = G_(i:j) +P_(i:j) * C_j
G_(i:i-1) = G_i + P_i * G_(i-1) P_(i:i-1) = P_i * P_(i-1)
example - 4 bit Blocks


그림에서 알 수 있듯이 RCA와 달리 CLA에서는 G와 P를 계산하여 C out을 곧바로 계산할 수 있습니다.
Carry-Lookahead Adder Delay
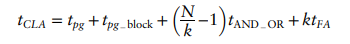
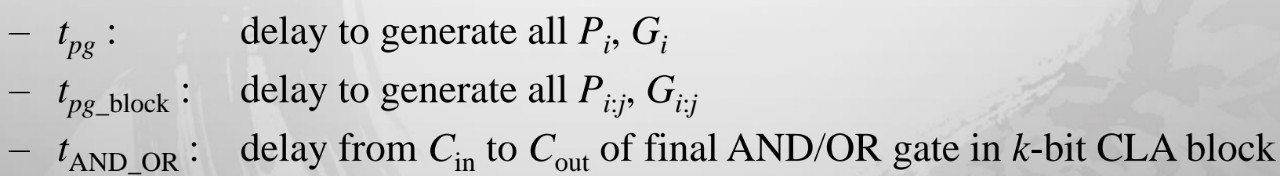
Example 5.1 Compare the delays of a 32-bit ripple-carry adder and a 32-bit carry-lookahead adder with 4-bit blocks. Assume that each two-input gate delay is 100 ps and that a full adder delay is 300 ps. Solution: According to Equation 5.1, the propagation delay of the 32-bit ripplecarry adder is 32 × 300 ps = 9.6 ns. The CLA has t_pg = 100 ps, t_pg_block = 6 × 100 ps = 600 ps(6개의 AND, OR gate), and t_AND_OR = 2 × 100 ps (2개)= 200 ps.
According to Equation 5.6, the propagation delay of the 32-bit carry-lookahead adder with 4-bit blocks is thus 100 ps+ 600 ps + (32/4 − 1) × 200 ps + (4 × 300 ps) = 3.3 ns, almost three times faster than the ripple-carry adder.
Prefix Adder (PA)
CLA에서의 연산을 병렬적으로 수행하고, 그 결과를 재사용하면서 sum을 구하는 방법입니다.
모든 컬럼에 대해서 각각 Carry를 미리 계산하는 것입니다.
- Sum

이때, G_-1을 정의하여 C_in을 대체하면, G_-1 = C_in, P_-1 = 0 입니다.
따라서 C_i-1 = G_(i-1:-1)입니다. - Generate and Propagate Signal

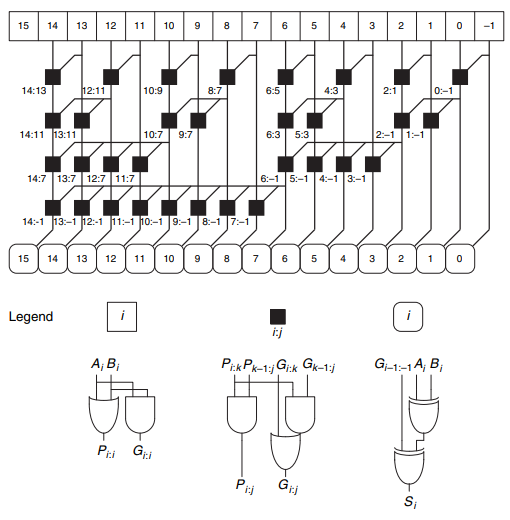
연산을 빠르게 하기 위해서는 이러한 prefix들을 빠르게 계산해야 합니다.
아래의 Schematic을 보면, 연산을 진행한 block을 재사용함으로써 연산으로 속도를 높힐 수 있습니다.
예를 들면, 6:-1을 살펴보면 해당 block은 14:-1,13:-1 그리고 쭉 이어서 7:-1까지의 block들을 계산할 때 재사용된다. 14:-1의 경우 14:7과 6:-1를 통해 구할 수 있습니다.
Example
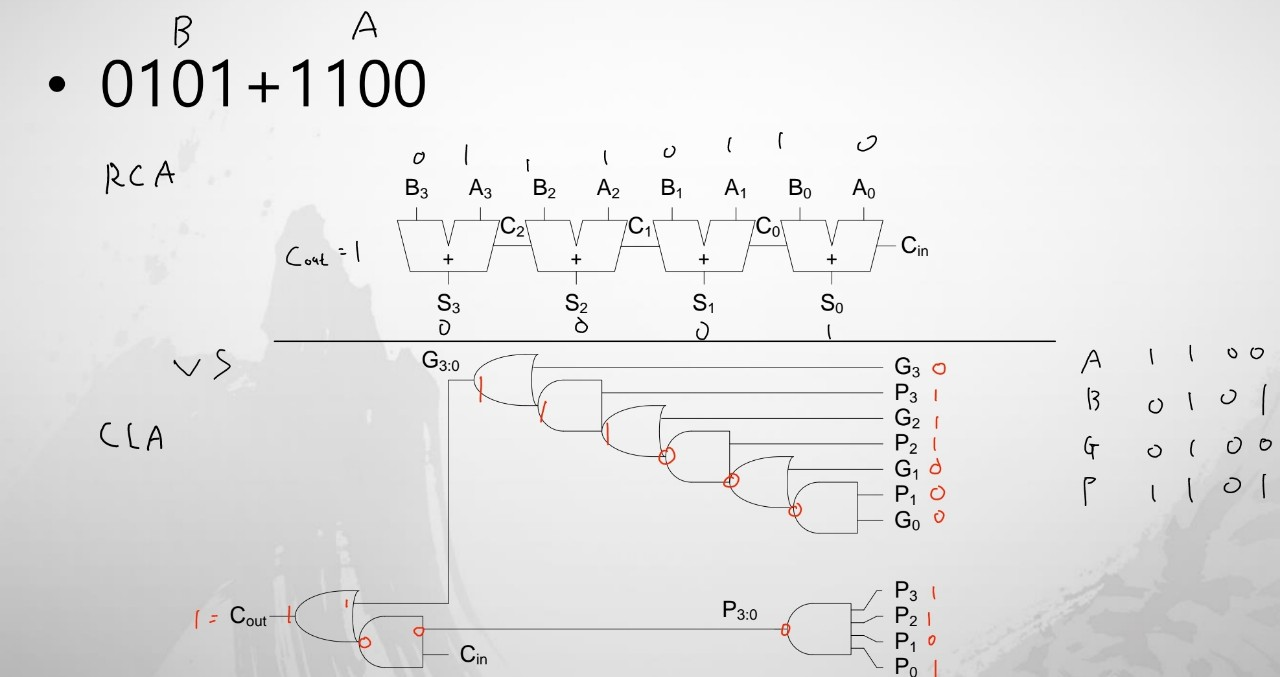
0101 + 1100
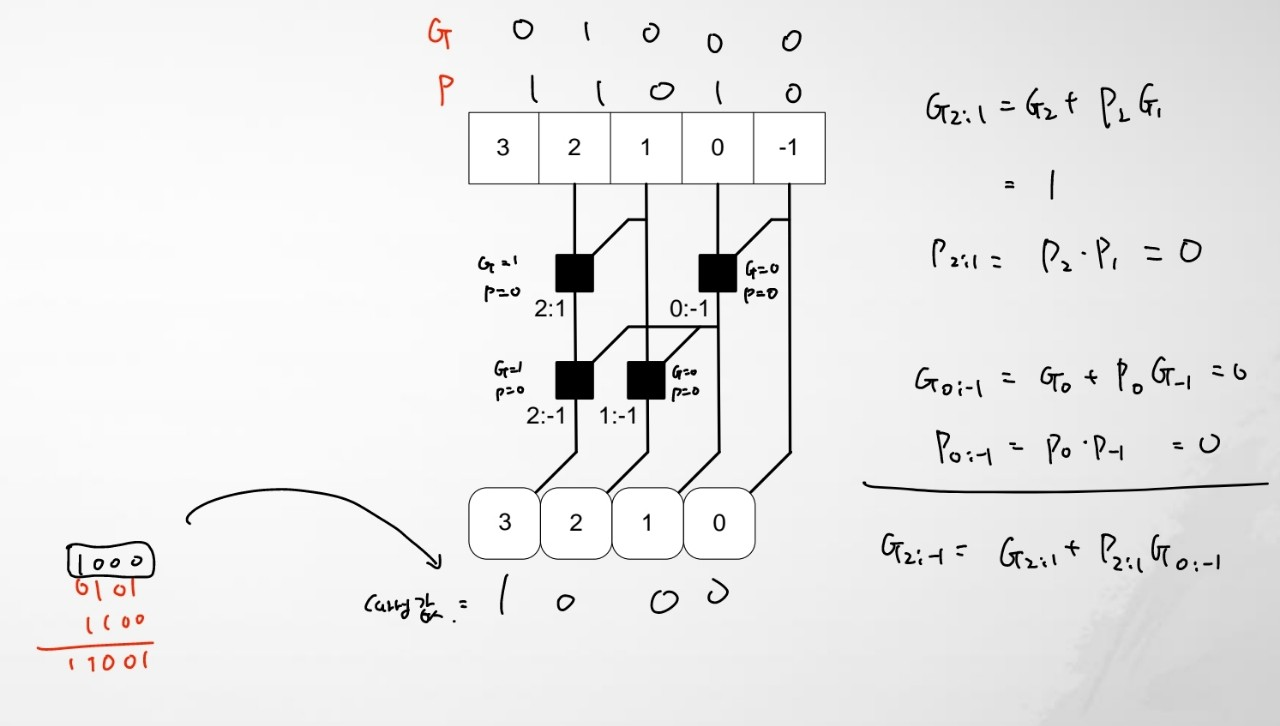
아래 계산된 Carry값을 보면, 왼쪽 하단에 따로 연산한 결과와 일치함을 확인할 수 있습니다.
Prefix Adder Delay
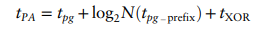

Example 5.2 PREFIX ADDER DELAY Compute the delay of a 32-bit prefix adder. Assume that each two-input gate delay is 100ps. Solution: The propagation delay of each black prefix cell tpg_prefix is 200 ps (i.e., two gate delays). Thus, using Equation 5.11, the propagation delay of the 32-bit prefix adder is 100 ps + log2(32) × 200 ps + 100 ps = 1.2 ns, which is about three times faster than the carry-lookahead adder and eight times faster than the ripple-carry adder from Example 5.1. In practice, the benefits are not quite this great, but prefix adders are still substantially faster than the alternatives.
RCA, CLA, PA 비교

(2) Subtracter
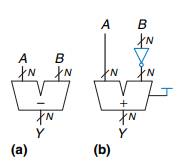
A-B를 구현하기 위해서는 B의 inverse를 취하여 1의 보수를 구하고, 여기에 1을 더해서 2의 보수를 구합니다. 이를 더해주어 뺄셈을 구현합니다.
(3) Comparator : Equality
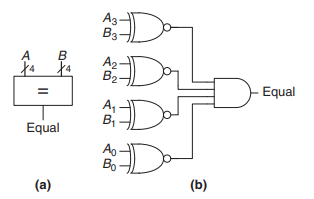
A == B를 구현하는 방법은 여러가지가 있습니다. 여기서는 XNOR을 이용하였는데, XNOR의 진리표를 작성해보면, 서로 같을 때 1이 나옵니다.
즉, 각 자리마다 XNOR gate를 연결하고, 모두 AND로 연결한다면 모든 자리에서 서로 같을 때만 최종 결과가 1이 나올 것입니다. XOR을 이용하여 구현해도 되고, 아니면 A - B = 0을 확인하여 구현하는 방법도 있을 것입니다.
(4) Comparator : Less Than
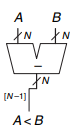
크기 비교를 위해서는 우선 A-B을 계산한 뒤, 최상위 bit인 [N-1]자리의 bit를 가져와서 확인하면 됩니다. MSB는 sign bit이기 때문에 이것이 0이냐 1이냐에 따라서 A와 B의 크기를 비교할 수 있습니다.
(5) Arithmetic Logic Unit (ALU)
위에서 설명한 여러 연산들을 한 번에 묶어서 표현한 것이 ALU입니다. 입력에 따라 그에 따른 연산을 수행하는 것입니다.
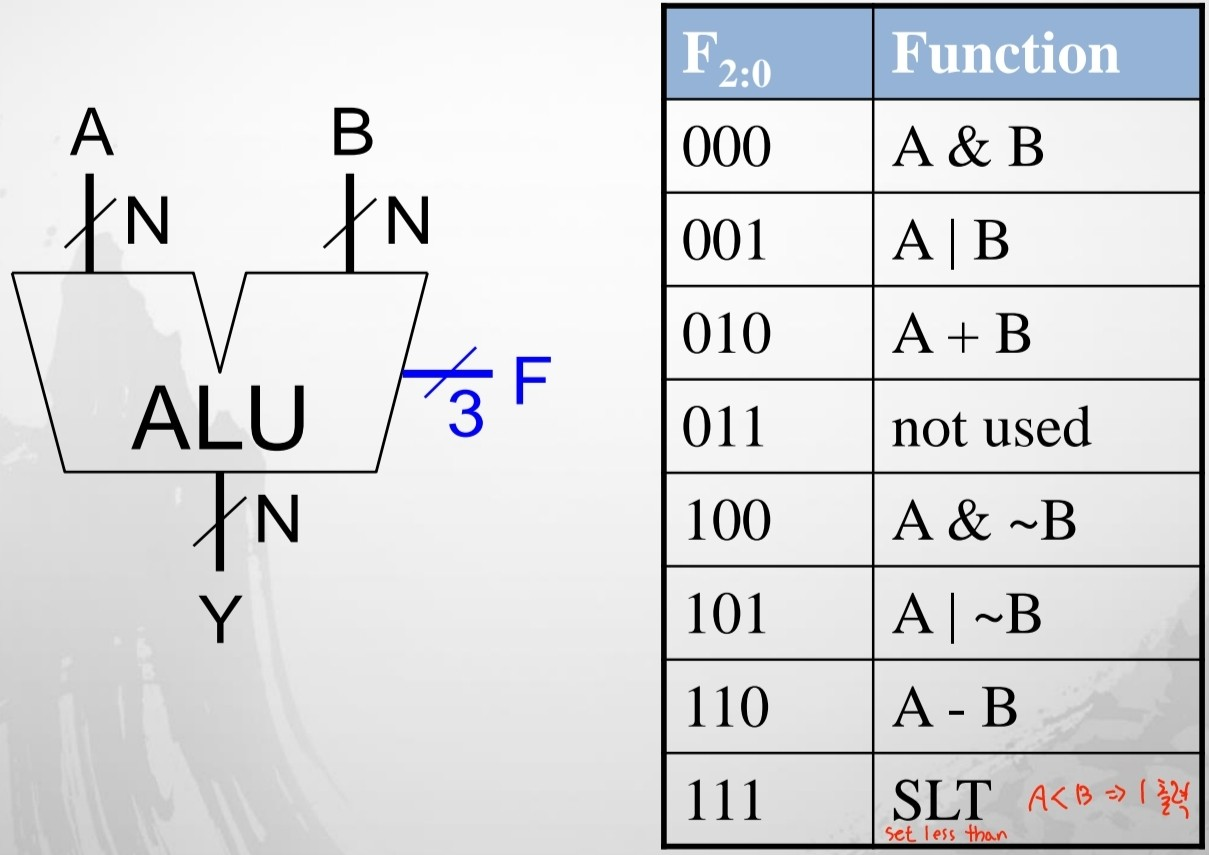

만약 F = 110이라면, 첫번째 MUX에 의해서 B의 inverse가 선택되고, 두번째 MUX에서는 “2”가 선택됩니다. 이때, F2가 더하기 연산의 Carry in으로 들어가기 때문에 결국 최종적인 결과는 A + B의 inverse + 1입니다. 즉, 뺄셈인 A-B입니다.
SLT 예시도 살펴보면 아래와 같습니다.
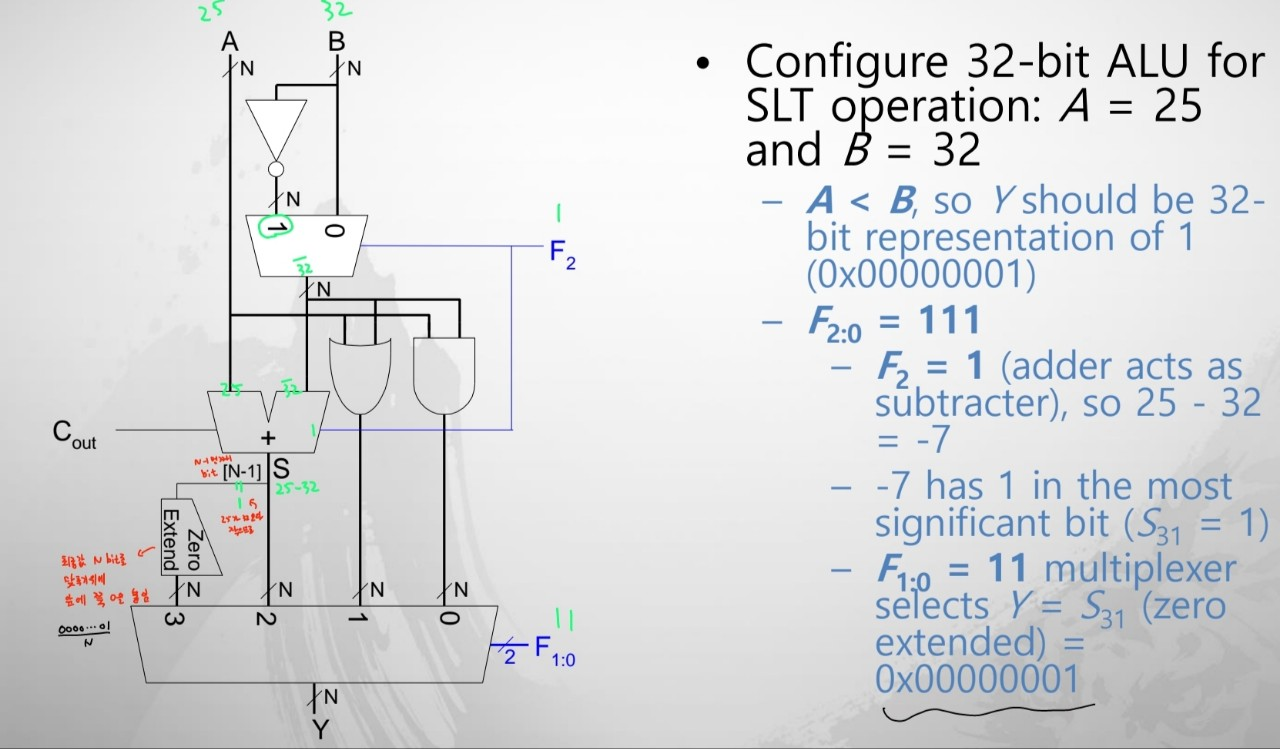
F2가 1이기 때문에 A-B 연산이 실행되고, 아래의 MUX에서 “3”자리가 선택됩니다. 해당 자리는 최상위 bit를 고른 뒤 앞에 N bit가 될 때까지 0을 붙인 결과를 반환합니다. 25는 32보다 작기 때문에 sign bit는 1이 될 것이고, 따라서 결과는 0000…1이고 이를 통해 SLT의 연산 결과로써 A가 B보다 작다는 것을 알 수 있습니다.
(6) Shifters, Rotator
- logical shift : 빈 자리를 그냥 0으로 채우는 방법 / >>(LSR), <<(LSL)
- arithmetic shift : shift전 sign bit를 shift 후 최상위 비트에 채우는 방법/ >>>(ASR), <<<(ASL)
- ROR, ROL
Example
11001 >> 2 = 00110
11001 << 2 = 00100
11001 >>> 2 = 11110
11001 <<< 2 = 00100
11001 ROR 2 = 01110
11001 ROL 2 = 00111
Shifter Design
- MUX로 구현하는 방법
shamt에 따라서 MUX에 의해서 출력이 결정됩니다.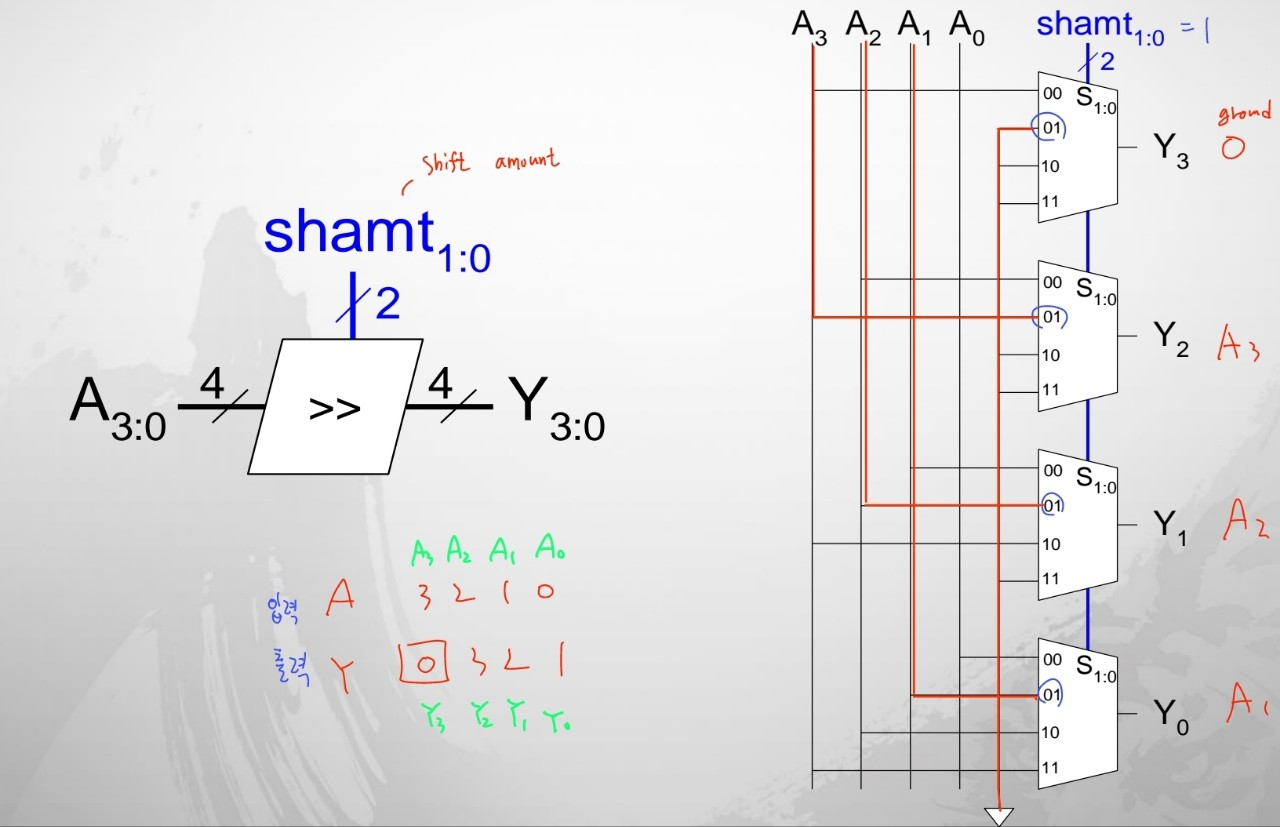
- transiter로 구현하는 방법
Decoder에 의해서 나오는 값에 따라서 해당하는 한 비트만 1로 만들어 shift를 구현합니다.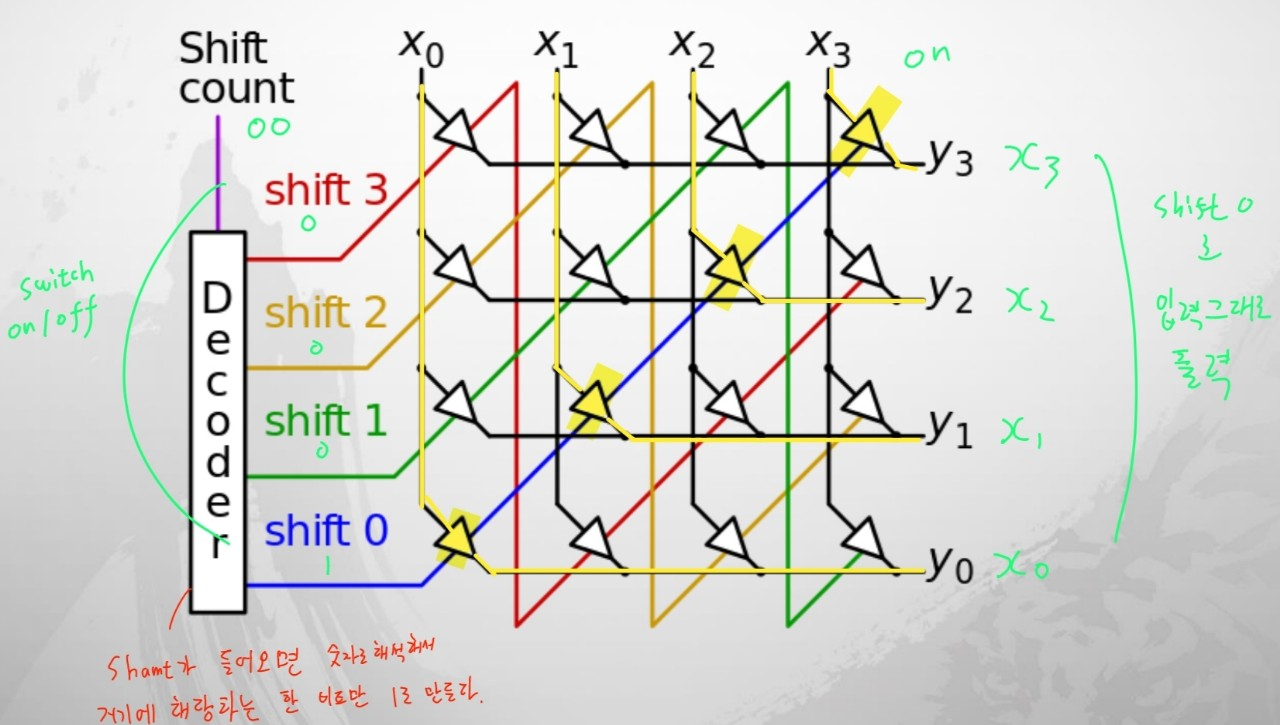
Shifter로 Multipliers와 Dividers 구현하기
곱셈은 logical shifter를 이용하고, 나눗셈은 arithmetic shifter를 이용하여 구현합니다.

Binary Division Algorithm

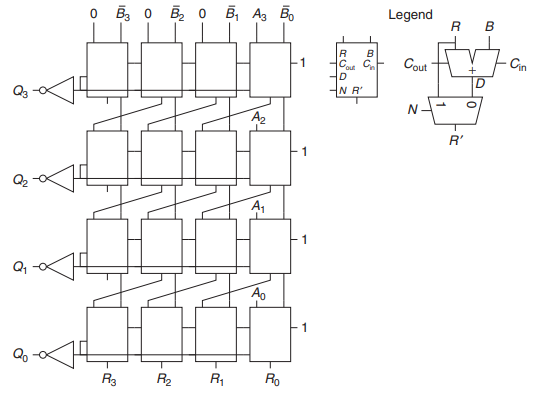
알고리즘을 살펴보면, R은 R’를 shift한 후 다음 A값을 붙여서 만들고, 그 결과와 B와의 차이를 구하여 몫과 다음 나머지를 구합니다.
Example
